Ответы 1.2 Представление чисел в компьютере, ГДЗ учебник информатика 8 класс Босова
Задание 2. Как в памяти компьютера представляются целые положительные и целые отрицательные числа?
При представлении со знаком самый старший (левый) разряд отводится под знак числа, а остальные разряды – под само число.Когда число положительное, то в знаковый разряд помещается 0, когда число отрицательное, то 1.
Задание 3. Любое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
Обычно вещественные числа важны при решении научных и инженерных задач. Алгоритм обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел. Для хранения в компьютере вещественных чисел выделяются разряды на хранение порядка числа, самого порядка, знака мантиссы и мантиссы.Задание 4. Представьте число 6310 в беззнаковом 8-разрядном формате.
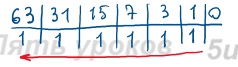
6310 = 1111112
В восьмиразрядном представлении имеет вид:

Задание 5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100Так как в знаковом разряде стоит 0, значит число положительное. Переведём 1001100 в десятичную систему счисления:
10011002 = 1*26 + 1*23 + 1*22 = 64 + 8 + 4 = 7610
Ответ: +76
б) 00010101
Так как в знаковом разряде стоит 0, значит число положительное. Переведём 10101 в десятичную систему счисления:
101012 = 1*24 + 1*22 + 1*20 = 16 + 4 + 1 = 2110
Ответ: +21
Задание 6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
Максимальное значение в 8-разрядном формате 255 (таблица приведена в учебнике с минимальным и максимальным значением в различных разрядностях).1) 4438 = 4*82 + 4*81 + 3*80 = 4*64 + 32 + 3 = 29110 Число нельзя сохранить в 8-разрядном формате.
2) 1010102 можно сохранить в 8-разрядном формате, так как задействованы 6 разрядом из 8-ми.
3) Число 25610 нельзя сохранить в данном формате.
Задание 7. Запишите следующие числа в естественной форме.
а) 0,3800456*102 = 38,00456б) 0,245*10-3 = 0,000245
в) 1,256900Е+5 = 1,256900*105 = 125690
г) 9,569120Е-3 = 9,569120*10-3 = 0,00956912
Задание 8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
1) 20100102Е-42) 201001,02Е-2
3) 0,20100102Е+4
4) 2,0100102Е+3
5) 201,00102Е+1
Задание 9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой – правильной дробью, имеющей после запятой цифру, отличную от нуля.
а) 217,93410 = 0,217934*103б) 7532110 = 0,75321*105
в) 0,0010110 = 0,101*10-2
Задание 10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
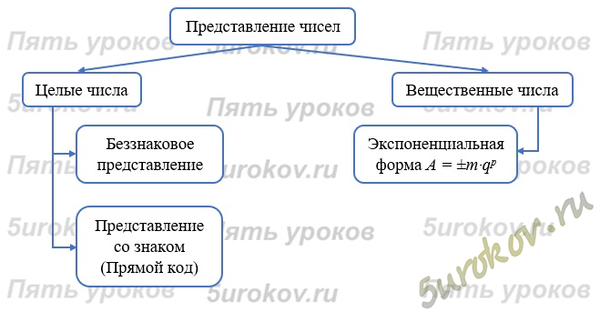 Решение заданий из учебника Информатика 8 класс Босова, параграф 1.2. Представление целых чисел, представление вещественных чисел.
Решение заданий из учебника Информатика 8 класс Босова, параграф 1.2. Представление целых чисел, представление вещественных чисел.
