Предмет: Информатика
ГДЗ Учебник по Информатике 8 класс БосоваОтветы на тест Элементы теории множеств и комбинаторики по Информатике 8 класс Босова
ЧАТ-БОТ: ГДЗ с нейронкой
8_Тест «Элементы теории множеств и комбинаторики». Выберите нужный вариант:
1) В одном множестве 40 элементов, в другом – 30. Какое максимальное количество элементов может быть в их объединении?
Ответ: 70
2) Сколько разных пятибуквенных слов можно составить в двоичном алфавите?
Ответ: 32
Решение: 25 = 32
3) Даны множества А и В. Множество, состоящее из их общих элементов называется…
объединением множеств А и В
дополнением множества А до В
пустым множеством
пересечением множеств А и В
дополнением множества В до А
Ответ: пересечением множеств А и В
4) На рисунке изображены отрезки AB и CD. Укажите пересечение этих отрезков:

CD
AC
Ø
AD
AB
BC
Ответ: Ø
5) На рисунке изображено несколько отрезков. Укажите дополнение отрезка BC до BD:

CD
AD
AB
AC
BC
Ответ: CD
6) Пересечением множеств А и В обозначается:
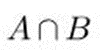
7) Пусть множество А является подмножеством множества В. Это обозначается:
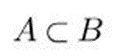
8) Имеется неограниченно много бусин пяти разных цветов. Сколько разных цепочек из трёх бусин можно из них составить?
Ответ: 125
Решение: 53 = 125
9) Укажите наименьшее k для которого в двухбуквенном алфавите можно составить не менее 50 разных k-буквенных слов:
7
5
6
50
Ответ: 6
Решение: При k=5 в двухбуквенном алфавите будет 32 разных пятибуквенных слов, а при k=6 будет 64. Нам необходимо минимум 50 разных слов, то есть ответ будет удовлетворять при k=6.
Ответ: 70
2) Сколько разных пятибуквенных слов можно составить в двоичном алфавите?
Ответ: 32
Решение: 25 = 32
3) Даны множества А и В. Множество, состоящее из их общих элементов называется…
объединением множеств А и В
дополнением множества А до В
пустым множеством
пересечением множеств А и В
дополнением множества В до А
Ответ: пересечением множеств А и В
4) На рисунке изображены отрезки AB и CD. Укажите пересечение этих отрезков:

CD
AC
Ø
AD
AB
BC
Ответ: Ø
5) На рисунке изображено несколько отрезков. Укажите дополнение отрезка BC до BD:

CD
AD
AB
AC
BC
Ответ: CD
6) Пересечением множеств А и В обозначается:
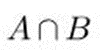
7) Пусть множество А является подмножеством множества В. Это обозначается:
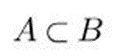
8) Имеется неограниченно много бусин пяти разных цветов. Сколько разных цепочек из трёх бусин можно из них составить?
Ответ: 125
Решение: 53 = 125
9) Укажите наименьшее k для которого в двухбуквенном алфавите можно составить не менее 50 разных k-буквенных слов:
7
5
6
50
Ответ: 6
Решение: При k=5 в двухбуквенном алфавите будет 32 разных пятибуквенных слов, а при k=6 будет 64. Нам необходимо минимум 50 разных слов, то есть ответ будет удовлетворять при k=6.
1) На рисунке изображено несколько отрезков. Укажите дополнение отрезка CD до BD:

AB
AD
BC
AC
CD
Ответ: BC
2) В одном множестве 40 элементов, в другом – 30. Какое максимальное количество элементов может быть в их пересечении?
Ответ: 30
3) Сколько разных двухбуквенных слов можно составить в алфавите из пяти символов?
Ответ: 25
Решение: 52 = 25
4) Принадлежность элемента а множеству А обозначается:
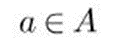
5) Имеется неограниченно много бусин трех разных цветов. Сколько разных цепочек из пяти бусин можно из них составить?
Ответ: 243
Решение: 35 = 243
6) Объединение множеств А и В обозначается:
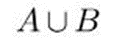
7) На рисунке изображены отрезки AB и AC. Укажите объединение этих отрезков:

AB
CD
AD
AC
BC
Ответ: AC
8) Даны множества А и В. Множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств называется…
пересечением множеств А и В
пустым множеством
дополнением множества В до А
дополнением множества А до В
объединением множеств А и В
Ответ: объединением множеств А и В
9) Укажите наименьшее k для которого в двухбуквенном алфавите можно составить не менее 100 разных k-буквенных слов:
5
100
6
7
Ответ: 7
Решение: При k=6 в двухбуквенном алфавите будет 64 разных шестибуквенных слов, а при k=7 будет 128. Нам необходимо минимум 100 разных слов, то есть ответ будет удовлетворять при k=7.

AB
AD
BC
AC
CD
Ответ: BC
2) В одном множестве 40 элементов, в другом – 30. Какое максимальное количество элементов может быть в их пересечении?
Ответ: 30
3) Сколько разных двухбуквенных слов можно составить в алфавите из пяти символов?
Ответ: 25
Решение: 52 = 25
4) Принадлежность элемента а множеству А обозначается:
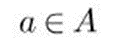
5) Имеется неограниченно много бусин трех разных цветов. Сколько разных цепочек из пяти бусин можно из них составить?
Ответ: 243
Решение: 35 = 243
6) Объединение множеств А и В обозначается:
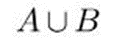
7) На рисунке изображены отрезки AB и AC. Укажите объединение этих отрезков:

AB
CD
AD
AC
BC
Ответ: AC
8) Даны множества А и В. Множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств называется…
пересечением множеств А и В
пустым множеством
дополнением множества В до А
дополнением множества А до В
объединением множеств А и В
Ответ: объединением множеств А и В
9) Укажите наименьшее k для которого в двухбуквенном алфавите можно составить не менее 100 разных k-буквенных слов:
5
100
6
7
Ответ: 7
Решение: При k=6 в двухбуквенном алфавите будет 64 разных шестибуквенных слов, а при k=7 будет 128. Нам необходимо минимум 100 разных слов, то есть ответ будет удовлетворять при k=7.
 ГДЗ: Учебник по Информатике 8 класс Босова
ГДЗ: Учебник по Информатике 8 класс Босова