Решение 1.3 Графические информационные модели по информатике 9 класс
Графические информационные модели
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Какими слайдами вы могли бы дополнить презентацию?
Презентация: Перейти2. Какие информационные модели относят к графическим?
К графическим информационным моделям являются простейшим видом моделей, которые передают внешние признаки объекты - размеры, форму, цвет.3. Приведите примеры графических информационных моделей, с которыми вы имеете дело:
а) при изучении других предметов;
б) в повседневной жизни.
а) Электрические схемы по физике, схема Куликовской битвы по истории, политическая карта мира, чертежи по черчению.б) График погоды на неделю, карта.
4. Что такое граф? Что является вершинами и рёбрами графа на рис. 1.6? Приведите примеры цепей и циклов, имеющихся в этом графе. Определите, какие два пункта наиболее удалены друг от друга (два пункта считаются самыми удалёнными, если длина кратчайшего пути между ними больше, чем длина кратчайшего пути между любыми другими двумя пунктами). Укажите длину кратчайшего пути между этими пунктами.
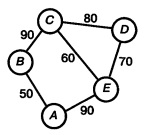
Граф - это объект изображенный с помощью вершин, а связи между ними - линиями (ребрами).
На данном рисунке вершины - города A, B, C, D, E; рёбра - дороги(линии) между ними.
Города B и D - наиболее удалены друг от друга. Длина кратчайшего пути между ними составляет 170.
5. Приведите пример системы, модель которой можно представить в форме графа. Изобразите соответствующий граф.
Пример графа: Персональный компьютер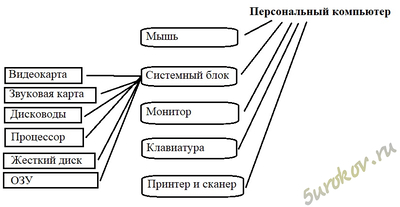
6. Грунтовая дорога проходит последовательно через населённые пункты А, В, С и D. При этом длина грунтовой дороги между А и В равна 40 км, между В и С — 25 км, и между С и D — 10 км. Между А и D дороги нет. Между A и С построили новое асфальтовое шоссе длиной 30 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге — 20 км/ч, по шоссе — 30 км/ч.
$IMAGE3$На графе черная линия - асфальтированное шоссе, а серая линия - грунтовая дорога.
По условию скорость велосипедиста по грунтовой - 20 км/ч, по шоссе - 30 км/ч.
От A до B можно добраться двумя способами: 1) 40 км по грунтовой дороге; 2) 30 по шоссе и 25 км по грунту.
Найдем время, которое может затратить велосипедист этими двумя способами(Расстояние делим на скорость).
1) 40:20 = 2 часа.
2) 25:20 = 1,25 часа по грунту, 30:30 = 1 час по шоссе, 2,25 часа займёт весь путь.
Ответ: 2 часа по грунтовой дороге в 40 км.
7. Составьте семантическую сеть по русской народной сказке «Колобок».
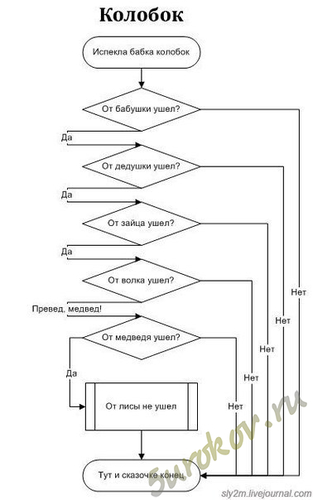
8. Что такое дерево? Моделями каких систем могут служить деревья? Приведите пример такой системы.
Дерево - это граф, в котором нет циклов. Все иерархические системы можно представить в виде дерева.Пример: генеалогическое дерево.
9. Сколько трёхзначных чисел можно записать с помощью цифр 2, 4, 6 и 8 при условии, что в записи числа не должно быть одинаковых цифр?
246; 248; 264; 284; 268; 286426; 428; 462; 468; 482; 486
624; 628; 642; 648; 682; 684
824; 826; 842; 846; 862; 864
Всего 24 числа.
10. Сколько существует трёхзначных чисел, все цифры которых различны?
Всего цифр 10: 0,1,2,3,4,5,6,7,8,9В трёхзначном числе три места
На первое можно поставить любую из девяти цифр( 0 нельзя)- 9 способов
На второе место останется 8 цифр + 0 = 9 цифр - 9 способов
На третье место 8 цифр, - 8 способов
Всего 9·9·8=648 чисел
11. Для составления цепочек используются бусины, помеченные буквами А, В, С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква гласная, и любая согласная, если первая согласная. На третьем месте — одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Сколько цепочек можно создать по этому правилу?
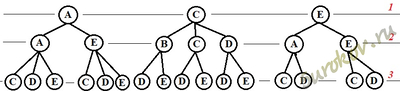
Составляем дерево вариантов и мы получаем:
Ветки начинающиеся с A: AAC AAD AAE; AEC AED AEE.
Ветки начинающиеся с C: CBD CBE; CCD CCE; CDD CDE.
Ветки начинающиеся с E: EAC EAD; EEC EED.
Ответ: 16 вариантов
12. Два игрока играют в следующую игру. Перед ними лежит куча из 6 камней. Игроки берут камни по очереди. За один ход можно взять 1, 2 или 3 камня. Проигрывает тот, кто забирает последний камень. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
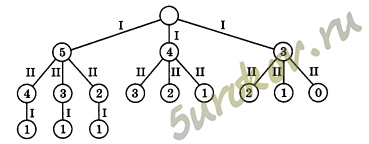
При безошибочной игре выигрывает первый игрок. Своим первых ходом он должен взять один камень. В куче остается пять камней. Какой бы ход ни сделал второй игрок, в куче останется 4, 3 или 2 камня. Это позволяет первому игроку своим вторым ходом оставить в куче ровно один камень, его и должен будет забрать своим вторым ходом второй игрок.
